Wenn «Gott würfelt», würfelt er nicht «unendlich»
Der Physiker Valentin Hirschi geht mit seiner Forschung einem neuen Ansatz für quantenfeldtheoretische Berechnungen nach. Genauere Vorhersagen für Experimente am Teilchenbeschleuniger am CERN sollen die innere Funktionsweise des Universums besser verstehen helfen.
Die Förderinstrumente Eccellenza und PRIMA des Schweizerischen Nationalfonds SNF ermöglichen hochqualifizierten Forschenden, ihre Projekte im Rahmen einer Assistenzprofessur an einer Schweizer Universität umzusetzen. In einer Serie von Interviews stellen wir sechs neu ausgezeichnete Forschende und ihre Projekte vor.

Sie haben eine «Eccellenza Professorial Fellowship» vom Schweizerischen Nationalfonds empfangen. Was bedeutet es für Sie, dieses Forschungsstipendium zu erhalten?
In erster Linie ist es ein Beweis für das Vertrauen, das die Gemeinschaft in meine Forschung setzt. Dafür bin ich sehr dankbar. Es wird mir ermöglichen, ein Team aufzubauen, um das volle Potenzial meines Projekts auszuschöpfen.
Ich freue mich darauf, eine neue Generation von Praktikerinnen und Praktikern auszubilden und ihnen mein Wissen über die Hochenergiephysik im Allgemeinen und ihre rechnerischen Aspekte im Besonderen zu vermitteln. Die grundlegenden Theorien der Physik sind im Laufe der Zeit immer abstrakter geworden, und ich glaube, dass ihr tiefes Verständnis eng mit der Fähigkeit zusammenhängt, ihre logischen Implikationen – oft quantitativ – zu berechnen.
Sie wurden vom SNF für Ihr Forschungsprojekt «Ein neuer Ansatz für perturbative Berechnungen in der Quantenfeldtheorie» ausgewählt. Worum geht es in dem Projekt?
Wenn wir vorhersagen wollen, wie sich eine Billardkugel von Punkt A nach B auf dem Tisch bewegt, denken wir nur an ihren geraden, den so genannten «klassischen» Weg. Wenn sich hingegen Teilchen bewegen und zusammenstoßen, müssen wir die Wahrscheinlichkeiten für alle möglichen Wege, auf denen der Prozess stattfinden kann, zusammenrechnen. Die Bahnen, die nicht gerade sind, tragen zwar weniger dazu bei, aber sie tragen dennoch bei!
In unserer kontinuierlichen Raumzeit nimmt diese Summe die Form eines Integrals an. In den traditionellen Ansätzen werden diese Integrale in Teile zerlegt, die bis ins Unendliche gehen. Im Laufe des letzten halben Jahrhunderts haben Mathematiker und Physikerinnen daran gearbeitet, Wege zu finden, diese Unendlichkeiten formal zu charakterisieren und zu regulieren – mit dem Ziel sie aufzuheben, wenn alle Teile der Berechnung wieder zusammengefügt werden.
In meiner Forschung wird eine alternative Formulierung mit dem Namen «Local Unitarity» vorgeschlagen, die diese Trennung vermeidet und jeden Term endlich werden lässt. Dies bietet praktische Vorteile bei der numerischen Auswertung der Integrale. Vielleicht noch wichtiger ist jedoch, dass es auch neue theoretische Erkenntnisse darüber liefert, warum, wenn Gott «würfelt», um Einstein zu paraphrasieren, er nie «unendlich» zu erhalten scheint.
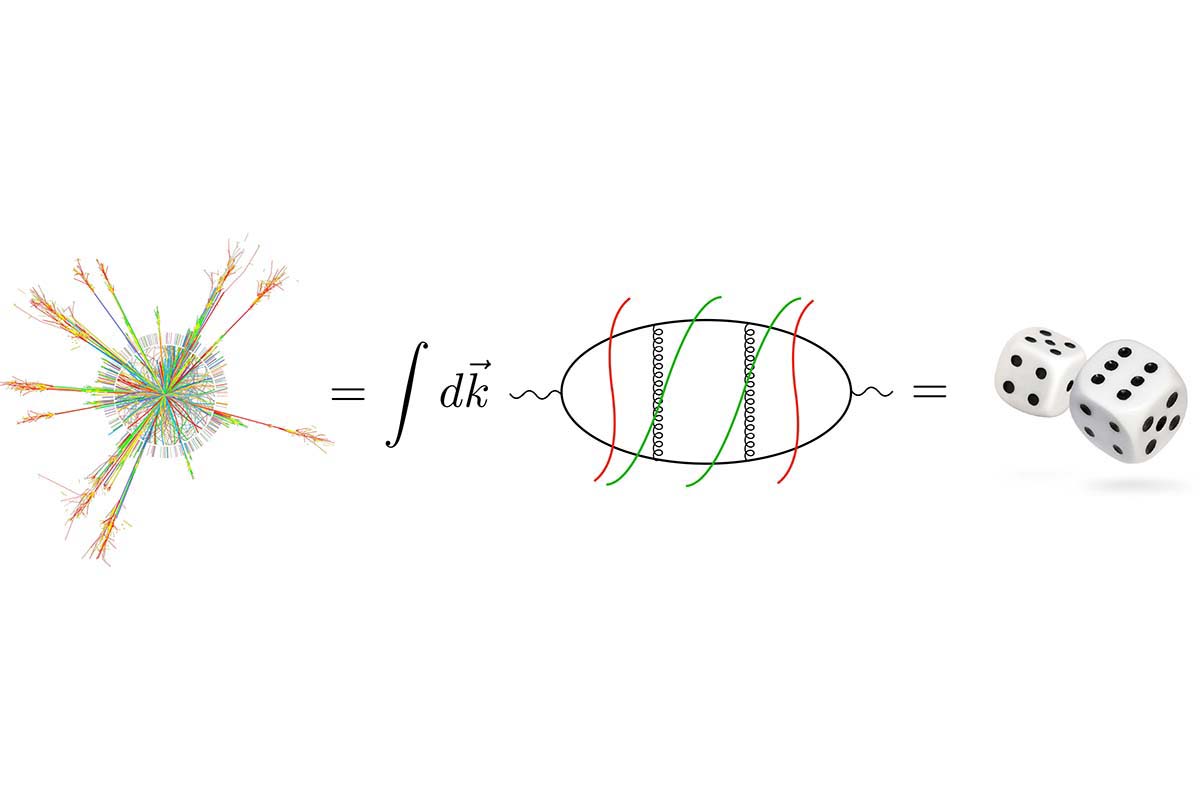
Weshalb haben Sie die Universität Bern für Ihr Projekt gewählt?
Simulationen von Teilchenbeschleuniger-Experimenten erfordern Fachwissen in einer Vielzahl von Aspekten der Quantenfeldtheorie, die für verschiedene Energieregime relevant sind. Meine Forschung befasst sich nur mit einem Teil davon. Diesen Teil hoffe ich in das Gesamtparadigma zu integrieren, unter anderem in Zusammenarbeit mit den zahlreichen Expertinnen und Experten am Institut für Theoretische Physik der Universität Bern. Die zentrale Lage der Universität Bern und ihre Nähe zum CERN bei Genf machen sie zu einem idealen Ort für meine Aktivitäten.
Worin besteht die gesellschaftliche Relevanz Ihres Projekts?
Aristoteles glaubte, dass schwerere Gegenstände schneller fallen als leichtere. Galilei hingegen verstand, dass Objekte auf der Erde einer gleichmässigen Abwärtsbeschleunigung unterliegen. Stellen Sie sich vor, diese beiden Geistesgrössen denken sich gemeinsam ein Experiment aus, um ihre Behauptungen zu überprüfen: Sie messen sorgfältig die Zeit, die ein Zahnstocher benötigt, um aus einer Höhe von 5 Metern zu fallen, und messen 1,1 Sekunden.
Der Luftwiderstand ist nicht vernachlässigbar und schwer zu berechnen, so dass Galileis hypothetische Berechnungen vorhersagen, dass der Zahnstocher in 1,2 ± 0,12 Sekunden fällt – also mit 10 % Unsicherheit –, während Aristoteles nur 1 Sekunde vorhersagt, allerdings mit der gleichen Unsicherheit. Das ist ein Unentschieden! Aufgrund der Ungenauigkeit ihrer Vorhersagen ist das Experiment nicht schlüssig.
Die Experimente am Teilchenbeschleuniger «Large Hadron Collider» am CERN sind insofern ähnlich, als dass die Vorhersagen für das, was beobachtet wird, genau genug sein müssen, um verschiedene Theorien der fundamentalen Physik unterscheiden zu können. In meiner Forschung wird ein neuer Weg vorgeschlagen, die sehr komplizierten Berechnungen der Quantenfeldtheorie durchzuführen, die diesen Vorhersagen zugrunde liegen, um ihre Genauigkeit zu verbessern und unsere Chancen zu erhöhen, die innere Funktionsweise des Universums weiter zu verstehen.
Über Valentin Hirschi
Prof. Dr. Valentin Hirschi promovierte 2013 an der EPFL in Physik. Anschliessend absolvierte er ein erstes Postdoc am SLAC (2013-2017), einem nationalen US-Labor, das von der Stanford University betrieben wird. Sein zweites Postdoc absolvierte er an der ETH Zürich (2017-2020), bevor er im Oktober 2020 seine derzeitige Position als Senior Fellow in der Theorieabteilung in der Europäischen Organisation für Kernforschung CERN antrat. Prof. Hirschi forscht über numerische Methoden in der Computerphysik und perturbative Quantenfeldtheorie für Anwendungen bei Kollisionssimulationen.
SNF Eccellenza Professorial Fellowships
SNF Eccellenza Professorial Fellowships richten sich an hoch qualifizierte Forschende, die eine permanente Professur anstreben. Eccellenza ermöglicht ihnen, ihr Ziel als Assistenzprofessorin oder Assistenzprofessor mit einem grosszügig ausgestatteten Forschungsprojekt unter ihrer Leitung und einem eigenen Team an einer Hochschule in der Schweiz zu erreichen. Eccellenza deckt das Salär der Beitragsempfängerin oder des Beitragsempfängers auf dem Niveau einer lokalen Assistenzprofessur und Projektmittel von bis zu 1'000'000 Franken für fünf Jahre ab. Im Jahr 2021 wurden vom Eccellenza-Programm vier Forschende an der Universität Bern ausgewählt.
SNF PRIMA
PRIMA-Beiträge richten sich an hervorragende Forscherinnen, die ein hohes Potenzial für eine Professur aufweisen. PRIMA-Beitragsempfängerinnen sind mindestens auf dem Niveau einer Gruppenleiterin angestellt und führen ein Forschungsprojekt mit einem eigenen Team an einer Schweizer Forschungsinstitution durch. Ein PRIMA-Beitrag umfasst das Salär der Beitragsempfängerin sowie Projektmittel für eine Dauer von fünf Jahren. Während des PRIMA-Beitrags ist es möglich, einen Aufenthalt an einer anderen Institution zu planen. Mit diesem kompetitiven Beitrag profilieren sich die PRIMA-Beitragsempfängerinnen für die nächste Stufe ihrer akademischen Karriere: Eine Professur. Wird eine PRIMA-Beitragsempfängerin während der Beitragsdauer auf eine Professur berufen, können die verbleibenden Mittel an den neuen Arbeitsort transferiert werden. Im Jahr 2021 wurden vom PRIMA-Programm zwei Forscherinnen an der Universität Bern ausgewählt.
Zur Autorin
Maura Widmer ist Hochschulpraktikantin in der Abteilung Kommunikation & Marketing an der Universität Bern.