When "God plays dice", he does not roll infinity

Physicist Valentin Hirschi's research explores a new approach to quantum field theory calculations. More accurate predictions for experiments at the Large Hadron Collider at CERN should help to better understand the inner workings of the universe.

You have received an "Eccellenza Professorial Fellowship" from the Swiss National Science Foundation SNSF. What does it mean to you to receive this Fellowship?
First and foremost, it is a testimony of the trust that the community placed in my research, for which I am grateful.

It will also allow me to build a team which is necessary to realize the full potential of my project. I look forward to coordinating this effort by training a new generation of practitioners and instilling in them my views on High Energy Physics in general, and its computational aspects in particular. Fundamental theories of physics have become increasingly abstract over time, and I believe that their deep understanding is intimately related to one’s ability to compute, often quantitatively, their logical implications.

You have been selected from the SNF for your research project "A novel approach to perturbative computations in Quantum Field Theory". What is the project about?
When we think of predicting how a billiard ball goes from point A to B on the table, we only think of its straight, or so-called classical path. On the contrary, when particles move and collide, we must sum probabilities of following all possible paths. The paths that are not straight contribute less, but they do contribute nonetheless!

In our continuous space-time, this sum takes the form of an integral. In traditional approaches, these integrals are split into parts that evaluate to infinity. Over the last half century, mathematicians and physicists have been working to find ways to formally characterize and regulate these infinities - with the goal to properly realize their cancellation when all the parts of the computation are put back together.

My research proposes an alternative formulation, called "Local Unitarity", that avoids this separation and keeps each term manifestly finite. This offers practical advantages when it comes to the numerical evaluation of these integrals. Perhaps more importantly however, it also provides new theoretical insights on why when "God plays dice", he never seems to roll infinity. In other words, my research allows one to better understand how quantum field theories give finite predictions.

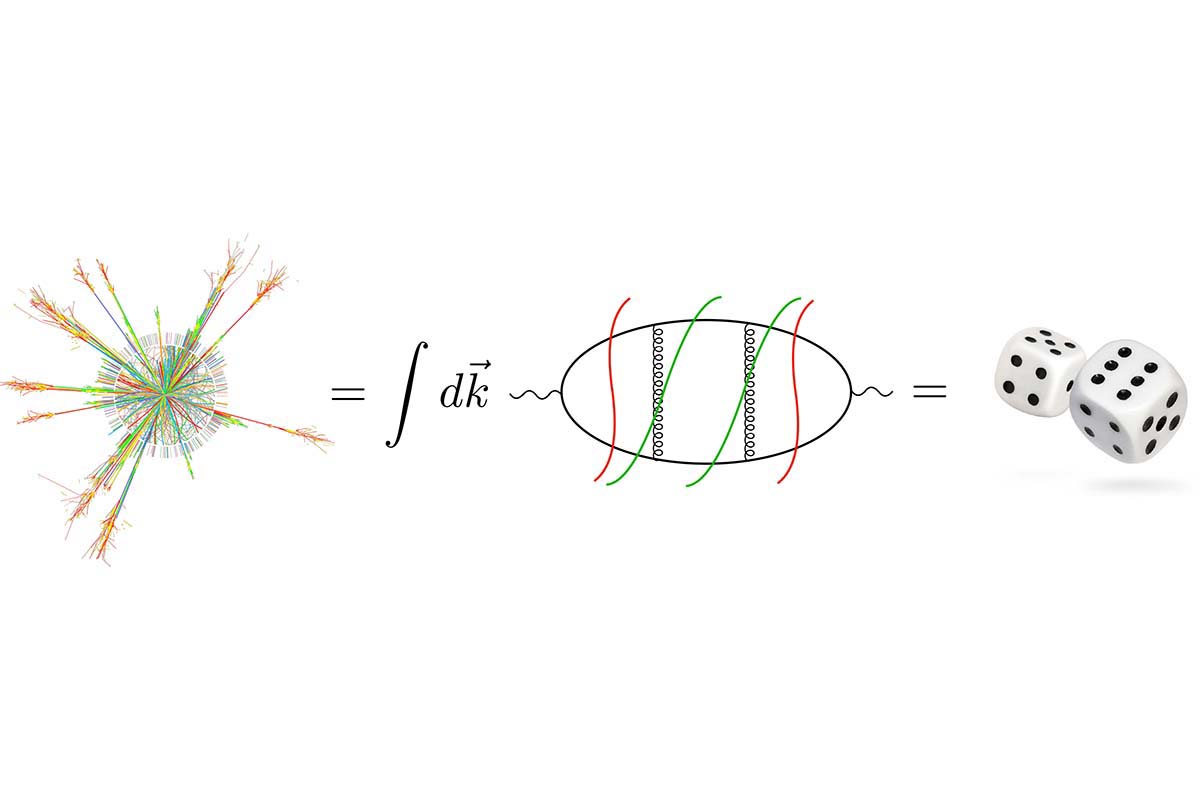
What made you chose the University of Bern for your Project?
Simulations of collider experiments require expertise in a multitude of aspects of Quantum Field Theory, relevant to different energy regimes.
My research tackles only a part of it, which I hope to integrate into the overall paradigm thanks in part to collaborations with the numerous experts at the Institute of Theoretical Physics of the University of. Bern.
The central location of the University of Bern and its proximity to CERN also makes it an ideal setting for my activities.

What is the social relevance of your project?
Aristotle believed that heavier objects fall faster than lighter ones. Instead, Galileo understood that objects on earth are subject to a uniform downward acceleration. Imagine that the two meet and devise an experiment to verify their claim, where they carefully measure the time for a toothpick to fall from a height of 5 meters and find it takes 1.1 second.
Air resistance is non-negligible and difficult to compute so that Galileo’s hypothetical calculations predict that the toothpick will fall in 1.2±0.12 second - so 10% uncertainty - whereas Aristotle predicts 1 second only, but with the same uncertainty.
That’s a tie! Because of the uncertainty plaguing their predictions, the experiment is inconclusive.

Experiments at the Large Hadron Collider at CERN are similar, insofar as predictions for what is being observed must be precise enough in order to be able to tell apart different theories of fundamental physics. My research proposes a novel way of carrying out the very complicated Quantum Field Theory calculations underlying these predictions to improve on their precision and improve our odds of further understanding the inner workings of the universe.